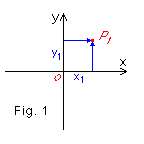
In his work La Geéometrie ("Geometry") René Descartes introduced the rectangular system of coordinates now known as the Cartesian coordinate system. Originally developed in two dimensions only, it defined the location of a point on a plane by its distance along two perpendicular axes from a defined origin (Figure 1): The distance from the origin O to the projection of the point P1 to the x-axis is x1, the distance from O to the projection of the point P1 to the y-axis is y1. The pair (x1, y1) are the Cartesian coordinates of P1.
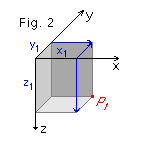
The principle was later extended into three dimensions (Figure 2), where it is often known as Euclidian coordinates. Three-dimensional rectangular coordinates use three axes x, y and z and define the location of a point P1 through the three distances x1, y1 and z1 along the respective axes. In oceanographic and meteorological applications the x-axis points towards east, the y-axis towards north and the z-axis downward (in oceanography) or upward (in meteorology).